Hexadecimal numbers

Binary numbers can be difficult to read, and difficult to type in without error. With a long string of ones and zeros, it is very easy to make a mistake. Hexadecimal notation makes this a lot easier.

Hexadecimal is often shortened to hex.

Hexadecimal

A group of 4 bits can take any value between 0 (0000 binary) and 15 (1111 binary).

In hexadecimal, we replace each group of 4 bits with a single digit to represent the value 0 to 15. Since we only have digits 0 to 9, we use letters A to E to represent values 10 to 15. Here is a table of binary, denary and hex values:

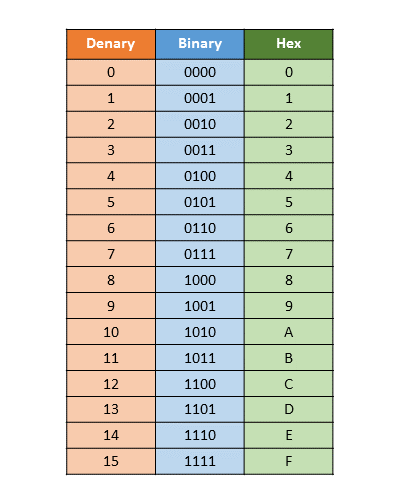
Hexadecimal numbers are often written in the form:

0x1A3C

Letters are usually not case sensitive, so you can also write

0x1a3c

Converting binary to hex

To convert the binary number 01101100 to hex:

• Split the binary into groups of 4 bits, in this case 0110 1100
• Look up each group in the table (binary -> hex), in this case we get 6 and C
• Put the digits together, e.g. 0x6C

Converting hex to binary

To convert the hex number 0xfe to binary:

• Look up each digit on the table (hex -> binary), in this case f gives us 1111, e gives us 1110
• Join the groups of 4 bits, in this case 11111110