Bitwise logical operations

You may be familiar with logic gates which use AND, OR, NOT and XOR logic.

You may also have used and, or, and not combinations in programming (for example if statements and while loops).

Bitwise logical operators follow the same rules but they act on the individual bits in a byte. They are useful for bit manipulation.

Bit fields

Often, a byte or word is used to contain a number value. But sometimes we are more interested in the individual bits within the byte.

For example, if you were making a computer game using a Raspberry Pi, Arduino or similar, you might connect push-buttons to the computers I/O (input/output) pins for left, right and fire functions.

When you check to see which buttons are pressed, you might get back a byte value, where:

• Bit 0 is set if the left button is pressed.
• Bit 1 is set if the right button is pressed.
• Bit 2 is set if the fire button is pressed.

So if the right button is pressed, you would get a value 00000010 binary (2 decimal).

Alternatively, if the left button and fire button were both pressed at the same time, you would get a value 00000101 binary (5 decimal).

If a byte (or a word of any size) is used as a collection of bits, we call it a bit field value. Bitwise logical operators are very useful for dealing with bit fields.

Bitwise AND

The bitwise AND operator often uses the symbol &.

It combines values by ANDing together each pair of bits in the two input bytes:

So in this example:

• Value A bit 0 is 0, Value B bit 0 is 0, so the result bit 0 is 0.
• Value A bit 1 is 0, Value B bit 1 is 1, so the result bit 1 is 0.
• Value A bit 2 is 1, Value B bit 2 is 0, so the result bit 2 is 0.
• Value A bit 3 is 1, Value B bit 3 is 1, so the result bit 3 is 1.
• etc

A particular result bit will only be 1 if both input bits are 1.

We can do this in pseudocode like this:

a = 01111100b
b = 01101010b
result = a & b
PRINT(result)

Which will print the value 01101000 binary (104 in denary).

Using bitwise AND as a bit mask

A bit mask is used to mask out unwanted bits in a byte, and just leave the ones you need. For example, suppose you have a byte value, and you want to find the value of the lowest hexadecimal digit. To do this you need to take the value of the lower 4 bits, ignoring the higher 4 bits.

For the AND function, we know that:

• ANDing anything with 0 is always 0, ie A & 0 = 0.
• ANDing anything with 1 leaves the value unchanged, ie A & 1 = A.

We can think of bitwise AND as a masking function. Here, we are using input B as a mask:

In this case:

• For the low 4 bits, where the mask bits are 1, the bit values in A are passed through to the result.
• For the high 4 bits, where the mask bits are 0, the bits in the result are forced to 0.

Bitwise OR

The bitwise OR operator often uses the symbol |.

It combines values by ORing together each pair of bits in the two input bytes:

So in this example:

• Value A bit 0 is 0, Value B bit 0 is 0, so the result bit 0 is 0.
• Value A bit 1 is 0, Value B bit 1 is 1, so the result bit 1 is 1.
• Value A bit 2 is 1, Value B bit 2 is 0, so the result bit 2 is 1.
• Value A bit 3 is 1, Value B bit 3 is 1, so the result bit 3 is 1.
• etc

A particular result bit will be 1 if either or both input bits are 1.

We can do this in pseudocode like this:

a = 01111100b
b = 01101010b
result = a | b
PRINT(result)

Which will print the value 01111110 binary (126 in denary).

Using bitwise OR to combine bit fields

Sometimes you might have two bit fields which need to be combined. For example:

• Value A has 4 bits of data in the lower 4 bits, and the upper 4 bits are set to 0.
• Value B has 4 bits of data in the upper 4 bits, and the lower 4 bits are set to 0.

We can think of bitwise AND as a masking function. Here, we are using input B as a mask:

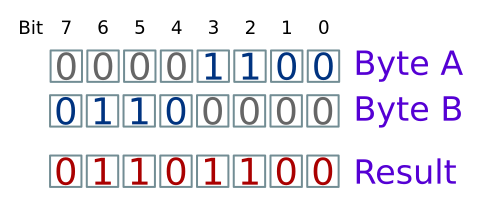
In this case:

• For the lower 4 bits of data in A are ORed with lower 4 bits of zeros in B, so the bit values in A are passed through to the result.
• For the upper 4 bits of data in B are ORed with upper 4 bits of zeros in A, so the bit values in B are passed through to the result.

Bitwise NOT

The bitwise NOT operation often uses the symbol ~. It takes one value, and returns the result of inverting each bit. For example:

a = 10101110b
result = ~a
PRINT(result)

prints 01010001 binary (each bit is the opposite of the input bit).

Bitwise XOR

The bitwise XOR operation often uses the symbol ^.

It behaves in a similar way to bitwise OR. The difference is that the output bit will be 1 if either (but not both) input bits are 1. The output bit will be zero if both inputs are 0, or if both inputs are 1.