Using algorithms

An algorithm is a step-by-step procedure for solving a particular problem.

We often use decomposition and abstraction to analyse the problem. We may try to recognise patterns to find existing techniques that might be applied top the problem.

Computer algorithms

When we design an algorithm for a computer to use, we must specify each step very precisely, so that it can be implemented as a computer program.

To define an algorithms we usually need to specify:

• The inputs
• The outputs
• The steps of the algorithm, usually in pseudocode or as a flowchart.

Turtle graphics - drawing a polygon

As an example, building on the previous sections, we will define an algorithm for drawing an n-sided polygon of a given size, using turtle graphics.

The inputs

The algorithm has 2 inputs:

• The number of sides for the polygon, n (integer).
• The radius of the polygon (floating point).

By radius, we mean the radius of the circle which encloses the polygon. In other words, the distance from the centre of the shape to one of its corners:

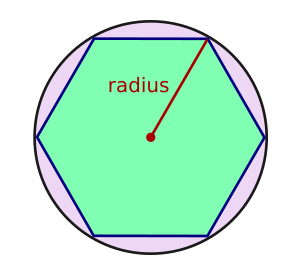
Clearly there are some constraints on the inputs:

• The number of inputs must be at least 3 (you cannot have a polygon with less than 3 sides).
• The radius must be greater than 0.

In theory, there is no limit to the number or sides, or the radius of the polygon. When you code up the algorithm, you might decided to set maximum values to avoid problems. For example, if you ask for a billion sides you might choose to give an error, otherwise it might take a very long time to draw! These limits aren't really part of the algorithm, they are called implementation details.

The outputs

The output of our algorithm is simply the polygon, drawn by the turtle. Depending of the type of turtle, it might draw on the screen, drag a pen on paper, or just move around on the floor.

The steps

We must calculate the angle the turtle must turn through at each corner. We have previously worked out that:

angle = 360.0/n

We must also calculate the length of each side. This is given by (See here):

length = 2 * radius * sin(angle/2)

We can then draw the shape like this:

repeat n times:
    forward(length)
    right(angle)

Angle gotcha

Angles in turtle graphics use degrees (1 full turn = 360 degrees). However, in most languages, the sine function expects the angle to be in radians (1 full turn = 2 PI radians). Th easiest solution is to define a second variable, the angle in radians:

angle_r = angle*PI/180

Example code

Here is the example code in Python. It can be easily rewritten in other languages that support turtle graphics:

import math
import turtle

n = 6
radius = 100

angle = 360/n
angle_r = angle*math.pi/180
length = 2*radius*math.sin(angle_r/2)

for i in range(n):
    turtle.forward(length)
    turtle.left(angle)

For further examples, see search algorithms and sort algorithms.